Do these 3 things before closing this tab:
1Fix the driver behind crashes, sound loss and screen glitches2Clear out junk files and repair common Windows errors3Scan for outdated or missing drivers - takes under a minuteThe Geeks Club is reader-supported. When you buy through links on our site, we may earn an affiliate commission. As an Amazon Associate I earn from qualifying purchases. Learn more
Recursion is the process of defining something in terms of itself. As it relates to Java programming, recursion is the attribute that allows a method to call itself. A method that calls itself is said to be recursive and Java supports recursion.
At first this may seem like a never ending loop, and it seems our method will never finish. This might be true is some cases, but in practice we can check to see if a certain condition is true and in that case exit (return from) our method. The case in which we end our recursion is called a base case. Additionally, just as in a loop, we must change some value and incrementally advance closer to our base case.
General shopping ads
Every recursion should have the following characteristics:
- A simple base case which we have a solution for and a return value.
- A way of getting our problem closer to the base case. i.e. a way to chop out part of the problem to get somewhat simpler problem.
- A recursive call which passes the simpler problem back into the method.
Advantages
The main to recursive methods is that they can be used to create clearer and simpler versions of several algorithms than can their iterative relatives. For example, the QuickSort sorting algorithm is quite difficult to implement in an iterative way.
Shopping ad
- Dimensions: 7.5" x 4.3" x 2.2". Compact size and lightweight make it easy to carry and put into your backpack, handbags or laptop bag without taking much space. Suitable for family use and daily organization. Note: Small mesh pockets are ideal for charging cords no longer than 3ft; longer cables (over 3ft) fit better in the larger compartments
- Quality Material: This electronic organizer travel case made of high quality durable waterproof oxford and soft sponge inside to secure your gadgets in place and deliver a quick access whenever you want. Water-resistant fabric protects your gear from unexpected splashes, keeping all your electronic essentials safe and secure
- Double Layers Design: This tech pouch features a double-layer interior design with 8 compartments, including multiple see-through mesh pockets and ample space to store your cords, cables, USB drives, cellphone, charger, mouse, flash drive and more, keeping all accessories neatly organized and tangle-free
- Practical and Convenient: Comes with a comfortable hand strap for easy carrying; You may carry it in your hand when heading out. Durable and smooth zipper closure keeps your favorite device securely, convenient for you to have quick access to the items inside the case
- Portable and Lightweight: The small size and lightweight design durable cable organizer pouch is a perfect choice when going on holiday, business trip, travel, office. Enjoy hassle-free travel without wasting time on tangled accessories. Great gift for yourself also a nice share with families and friends. (No include cords, electronic accessories)
Disadvantages
Recursive versions of many routines may execute a bit more slowly than the iterative equivalent because of the added overhead of the additional function calls. Many recursive calls to a method could cause a stack overrun. Because storage for parameters and local variables, it is possible that the stack could be exhausted. If this occurs, the java run-time system will cause an exception. However, you probably will not have to worry about this unless a recursive routine runs wild.
For example:
int myFactorial(int integer) {
if( integer == 1) {
return 1;
}
else {
return(integer*(myFactorial(integer-1);
}
}
Tail recursion is defined as occurring when the recursive call is at the end of the recursive instruction. This is not the case with my factorial solution above. It is useful to notice when ones algorithm uses tail recursion because in such a case, the algorithm can usually be rewritten to use iteration instead. In fact, the compiler will (or at least should) convert the recursive program into an iterative one. This eliminates the potential problem of stack overflow.
Shopping ad
- 【UPGRADED LAPTOP CLEANING KIT 】 The macbook cleaning kit computer screen cleaner comes with a number of accessories including a retractable large brush, polishing cleaning cloth X 2, keycap puller, metal pen tip, flocking sponge, thin soft brush, soft plastic lens cleaning pen, 5 replacing cloth, large cleaning microfiber cloth. You deserve the comprehensive computer cleaning kit keyboard vacuum at a low cost
- 【PROFESSIONAL KEYBOARD CLEANING KIT】 The laptop screen cleaner keyboard cleaner can pull out the keycaps of gaming keyboards and mechanical keyboards. A retractable keyboard brush works on laptops and keyboards, while the mini high-density brush is great for deep cleaning between keys for cleaning between flatter keys on a laptop, the metal pin tip gently removes any stains. This electronic cleaning kit macbook cleaner totally meets professional cleaning needs
- 【OFFICE DESK ACCESSORIES】This keyboard cleaner kit is easy to use and can clean your keyboard and electronic screen with just one swipe. Wiping with the 2mm thicken widen polishing cleaning cloth designed at a right angle for better fitting screen corners of computers with our recyclable cleaning spray, The laptop cleaner kit for macbook effectively absorbs stubborn stains, leaves no discoloration, no streaks, and no fiber shedding on the screens
- 【MULTIFUNCTIONAL TOOLS 】Mini soft brush and soft plastic lens cleaning pen are specially designed for DSLR camera screen, lens, and other delicate surfaces. 5 more cleaning cloths of it supplied for replacement. The flocking sponge is an excellent tool for cleaning earbuds charging cases, And the earbud cleaning kit is ideal. This electronics for college students is equivalent to 10 other electronic cleaning kit
- 【PORTABLE DESIGN & CLEANER TOOL】 The office supplies is compact in design, easy to carry, and you can easily take it anywhere. It's convenient to keep one in a drawer, one in your car, or in your bag and dorm. It is easy to use and can clean your keyboard and electronic screen with just one swipe. Is the college essentials cleaning tool for your friends, family, colleagues and students
This is not the case with head recursion, or when the function calls itself recursively in different places like in the Towers of Hanoi solution. Of course, even in these cases we could also remove recursion by using our own stack and essentially simulating how recursion would work.
What’s actually slowing this PC down?
Pick the symptom - the matching free tool is one click away.
In my example of factorial above the compiler will have to call the recursive function before doing the multiplication because it has to resolve the (return) value of the function before it can complete the multiplication. So the order of execution will be “head” recursion, i.e. recursion occurs before other operations.
Shopping ad
- Compatible Space: This electronics organizer bag features 2 zippered mesh pockets fits phones, standard power banks, 4 elastic loop pouches for small items, 2 elastic loop pouches for wireless headphones and small chargers. Elastic loops for phone charging cable. And specific slots for SD cards. Please check the size to ensure it meets your needs
- Lightweight Travel Accessories: The size of the electronic organizer travel case is 10.6" L x 7.5" W x 1.2" H, Compact but substantial size fits your intended bag or space. Suitable for traveling use and daily organization
- Keep Everything Organized: This compact travel organizer features dedicated compartments for your phone charger, cables, and tech accessories, keeping them tangle-free and ready to go. You can find travel accessories quickly, no chasing cords in your pack anymore
- Durable Travel Essentials: Features double zippers for easy access, elastic loops with non-slip grips for daily protection. Organizer for office use and traveling, (Not including cords, electronic accessories). It can serve as a travel checklist. Before you leave a place, just open the case and check if everything is there, preventing you from leaving things behind
- Versatile Use: Its practicality and convenience make it a travel essential bag. It is suitable for a weekend trip, business trip, and travel. This organizer pouch is suitable for office, business, daily use and can be given as a gift for friends, family, or men, for birthdays, Valentine's Day, Christmas Day, Father's Day
To convert this to tail recursion we need to get all the multiplication finished and resolved before recursively calling the function. We need to force the order of operation so that we are not waiting on multiplication before returning. If we do this the stack frame can be freed up.
Previously you have seen our Java program to calculate factorial of an integer.
Shopping ad
- Universal fit: ColorCoral cleaning gel, simple and convenient cleaning kits for PC/laptop keyboard and other rugged surface, such as the car vent, camera, printer, telephone, calculator, Instrument, speaker, air conditioner, TV and other appliances
- Safe cleaning gel: The keyboard cleaner gel is made from natural gel, no sticky to hands, smells sweet with lemon fragrance, no stimulation to skin
- Easy dust cleaning: Make sure your hands are dry and clean, knead the cleaning gel into a ball, press the cleaning gel slowly into the keyboard, car vent and rugged surface till the cleaning gel could touch the bottom and then pull out, the dust would be carried away with the cleaning gel
- Reusable: The keyboard cleaning gel could be used repeatedly till the color turn to dark or it become sticky, then you have to replace the cleaning gel with a new one. After cleaning, please stock the cleaning gel in cool place. (Note: Don’t wash the gel in water.)
- In the package: 1 can of universal cleaning gel, we provide the cleaning gel with brand new, if you find the package broken, the cleaning gel dirty, or any other quality issues, please email us through message, we provide you new one soon
The proper way to do a tail-recursive factorial is this:
Recommended Free Tools
int factorial(int number) {
if(number == 0) {
return 1;
}
factorial_i(number, 1);
}
int factorial_i(int currentNumber, int sum) {
if(currentNumber == 1) {
return sum;
} else {
return factorial_i(currentNumber - 1, sum*currentNumber);
}
}
Notice that in the call return factorial_i(currentNumber – 1, sum*currentNumber); both parameters are immediately resolvable. We can compute what each parameter is without waiting for a recursive function call to return. This is not the case with the previous version of factorial. This streamlining enables the compiler to minimize stack use as explained above.
Shopping ad
- Award-Winning Compact Design & EDC-Ready Gift Choice: Weighing only 0.09 lb and sized like a credit card, this compact laser measure is designed for everyday carry. It slips easily into a pocket, tool pouch, or bag, and can attach to a keychain for quick access wherever you go. Its minimalist design, premium tactile finish, and practical one-button measuring make it a useful EDC gadget for DIYers, real estate agents, homeowners, and tech enthusiasts. A thoughtful gift for men on any occasion
- One-Button Easy Measuring, Simple to Use: Designed with simple one-button operation, this compact laser tape measure makes quick measuring easy without complicated controls. Just press to measure room dimensions, furniture spacing, window height, wall décor placement, and everyday distances around the home. Ideal for users who want a smart, pocket-size measuring tool that fits naturally into an everyday carry (EDC) setup and feels intuitive, modern, and easy to use
- Fast & Accurate Indoor Measurements with Class 2 Laser: Measure distances from 0.16 ft to 98 ft with up to ±1/16 in / ±2 mm accuracy. With quick measurement response in about 0.2 seconds, HOTO helps you check spaces efficiently for home renovation, furniture layout, moving, decorating, craft projects, and DIY planning. Built with a Class 2 laser for everyday indoor measuring; use as directed and avoid direct eye exposure
- Low-Power OLED Display & USB-C Rechargeable Convenience: The low-power OLED display provides clear indoor readings while helping reduce battery drain. With USB-C rechargeable design, auto shut-off, and up to 1000 measurements per charge, this digital laser measure is built for repeated daily use without frequent battery replacement. Compact enough to keep in a drawer, toolbox, bag, or pocket
- Useful for Home, Work & Everyday Projects: From home renovation and furniture measuring to room planning, real estate checks, interior design, and light construction projects, this pocket-size laser distance measure is made for practical everyday use. Compact enough to keep in a drawer, toolbox, bag, or pocket, it is a stylish measuring tool that feels just as giftable as it is useful
You can also take the number from the user as a command line argument.
Independent reader supportYour contribution helps us test, update, and keep practical guides available for everyone.Java Recursion Program
class Factorial{
int fact(int n){
int result;
if ( n ==1)
return 1;
result = fact (n-1) * n;
return result;
}
}
class Recursion{
public static void main (String args[]){
Factorial f =new Factorial();
System.out.println("Factorial of 3 is " + f.fact(3));
System.out.println("Factorial of 4 is " + f.fact(4));
System.out.println("Factorial of 5 is " + f.fact(5));
}
}
Output
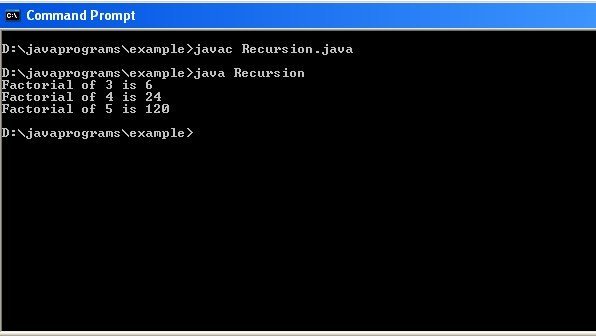
Explanation of the Java Code & Output
If you are unfamiliar with recursive methods, then the operation of fact() may seem a bit confusing. Here is how it works. When fact() is called with an argument of 1, the function returns 1; otherwise it returns the product of fact(n-1)*n. to evaluate this expression, fact() is called with n-1. This process repeats until n equals 1 and the calls to the method begin returning.
To better understand how the fact() method works, let’s go through a short example. When you compute the factorial of 3, the first call to fact() will cause a second call to be made with an argument of 2. This invocation will cause fact() to be called a third time with an argument of 2. This call will return 1, which is then be called a third time with an argument of 1. This call will return 1, which is then multiplied by 2 (the value of n in the second invocation). This result (which is 2) is then returned to the original invocation of fact() and multiply by 3 ( the original value of n). This yields the answer, 6. You might find it interesting to insert println() statements into fact() which will show at what level each call is and what the intermediate answers are.
When a method calls itself, new local variables and parameters are allocated storage on the stack, and the method code is executed with these new variables from the start. A recursive call does not make a new copy of the method. Only the arguments are new. As each recursive call returns, the old local variables and parameters are removed from the stack, and execution resumes at the point of the call inside the method.
Next we will learn how to deal with Array in Java.
Checkout more useful tutorials and definitive guidelines on Java programming here.
More shopping ads
Product prices and availability are accurate as of the date/time indicated and are subject to change. Any price and availability information displayed on Amazon at the time of purchase will apply.
